|
EN BREF
Avez-vous vu cela : Comment plier une veste de costume pour un rangement optimal |
Le tableau des valeurs de cosinus et sinus est un outil fondamental en trigonométrie, permettant de déterminer rapidement les valeurs de ces fonctions pour des angles spécifiques. Grâce à l’utilisation du cercle trigonométrique, on peut visualiser et comprendre les relations entre les angles et leurs valeurs trigonométriques. En spécialisant notre étude à des angles notables comme 0°, 30°, 45°, 60° et 90°, ce tableau facilite grandement les calculs et simplifie l’apprentissage des concepts trigonométriques. Que ce soit pour les étudiants débutants ou pour ceux qui cherchent à approfondir leurs connaissances, maîtriser ces valeurs demeure essentiel pour résoudre une multitude de problèmes mathématiques.
Le tableau des valeurs de cosinus et sinus constitue un outil fondamental en trigonométrie. Il permet de connaître rapidement les résultats des fonctions trigonométriques pour des angles spécifiques, facilitant ainsi les calculs dans divers domaines mathématiques. Cet article explore les définitions essentielles, les valeurs remarquables et l’interprétation graphique associée à ces fonctions.
Cela peut vous intéresser : Cuisson du poulpe congelé : astuces et conseils pour une préparation réussie
Les définitions de sinus et cosinus
Pour bien comprendre le tableau des valeurs de sinus et cosinus, il est crucial de commencer par leurs définitions. Le cosinus d’un angle réel x, noté cos x, est défini comme l’abscisse du point correspondant sur le cercle trigonométrique. En revanche, le sinus d’un angle réel x, noté sin x, est l’ordonnée de ce même point. Ces définitions sont essentielles pour analyser les propriétés et les comportements de ces fonctions.
Valeurs remarquables
Les valeurs de sinus et cosinus pour les angles spécifiques, tels que 0°, 30°, 45°, 60° et 90°, sont souvent désignées comme des valeurs remarquables. Par exemple :
- sin 0° = 0, cos 0° = 1
- sin 30° = 1/2, cos 30° = √3/2
- sin 45° = √2/2, cos 45° = √2/2
- sin 60° = √3/2, cos 60° = 1/2
- sin 90° = 1, cos 90° = 0
Ce tableau est non seulement utile pour les calculs rapides, mais il sert également de référence pour des calculs plus complexes impliquant des angles multiples.
Interprétation graphique
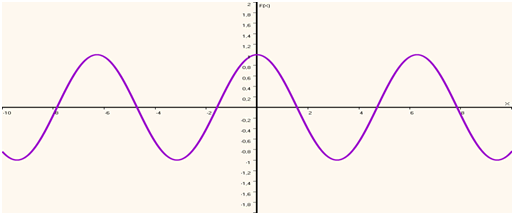
L’interprétation graphique des fonctions sinus et cosinus est également essentielle pour visualiser leurs comportements. Sur un cercle trigonométrique, les valeurs de sinus et cosinus peuvent être représentées comme les projections sur les axes x et y. Cette représentation aide à comprendre comment ces valeurs varient lorsque l’angle augmente, notamment :
- Le cosinus décroît de 1 à -1, avec des valeurs remarquables suivant une tendance particulière.
- Le sinus croît de 0 à 1, puis redescend à 0 et continue vers -1, suivant une courbe sinusoïdale.
Utilisation des tables de trigonométrie
Connaître les tables de trigonométrie permet d’accélérer le processus de détermination des valeurs trigonométriques. En visualisant un angle sur le cercle trigonométrique, il devient possible de déduire facilement le signe du sinus et du cosinus. Ces informations sont cruciales pour résoudre des problèmes d’angles complémentaires et supplémentaires.
Conclusion sur l’importance des valeurs de cosinus et sinus
Les valeurs de cosinus et sinus jouent un rôle prépondérant dans de nombreuses applications mathématiques et scientifiques. Que ce soit pour résoudre des équations trigonometriques, modéliser des phénomènes oscillatoires ou tout simplement naviguer dans les principes de base de la trigonométrie, une bonne maîtrise de ces tableaux de valeurs est indispensable. En les intégrant dans votre pratique, vous vous doterez d’un atout précieux pour tout étudiant ou professionnel dans le domaine des mathématiques.
| Angle (degrés) | Valeurs de cosinus | Valeurs de sinus |
| 0° | 1 | 0 |
| 30° | √3/2 | 1/2 |
| 45° | √2/2 | √2/2 |
| 60° | 1/2 | √3/2 |
| 90° | 0 | 1 |
| 120° | -1/2 | √3/2 |
| 135° | -√2/2 | √2/2 |
| 150° | -√3/2 | 1/2 |
| 180° | -1 | 0 |
| 210° | -√3/2 | -1/2 |
Dans le domaine de la trigonométrie, la compréhension des valeurs de cosinus et de sinus est essentielle pour résoudre de nombreux problèmes mathématiques. Ce tableau constitue un outil précieux pour les étudiants comme pour les professionnels, permettant de visualiser et d’apprendre rapidement les valeurs remarquables de ces fonctions trigonométriques. Nous allons plonger dans l’univers des angles et découvrir comment ces valeurs se manifestent.
Définitions des fonctions trigonométriques
Avant d’explorer le tableau, il est important de définir ces deux fonctions fondamentales. Le cosinus d’un angle est l’abscisse du point correspondant sur un cercle trigonométrique. On le note cos x. D’autre part, le sinus d’un angle représente l’ordonnée de ce point, notée sin x. Ces valeurs sont essentielles pour toute application trigonométrique.
Valeurs remarquables du sinus et cosinus
Lorsque l’on considère les angles entre 0° et 360°, certaines valeurs se démarquent comme des valeurs remarquables. Par exemple, pour des angles tels que 0°, 30°, 45°, 60° et 90°, nous pouvons facilement déterminer les valeurs exactes de sinus et cosinus. Ces valeurs sont souvent mémorisées et sont d’une grande utilité dans le calcul de problèmes trigonométriques complexes.
Utilisation du tableau trigonométrique
Pour utiliser le tableau des valeurs de cosinus et de sinus, il suffit de connaitre l’angle dont vous désirez les valeurs. En consultant le tableau, vous pouvez rapidement repérer le sinus et le cosinus de cet angle, simplifiant ainsi votre approche face à diverses circonstances mathématiques. Le cercle trigonométrique joue également un rôle crucial, vous permettant de visualiser les signes de ces valeurs selon le quadrant dans lequel se situe l’angle.
Élargir ses connaissances avec les tables de trigonométrie
En plus des valeurs de sinus et cosinus, il existe des tables contenant des informations sur d’autres fonctions trigonométriques telles que la tangente et la cotangente. Avoir accès à ces tables vous permet d’approfondir votre compréhension des relations entre les différentes fonctions trigonométriques. Cette connaissance est indispensable pour progresser dans le domaine des mathématiques appliquées.
- Angle (degrés): 0°, 30°, 45°, 60°, 90°
- Sinus: 0, 1/2, √2/2, √3/2, 1
- Cosinus: 1, √3/2, √2/2, 1/2, 0
- Angle (radians): 0, π/6, π/4, π/3, π/2
- Sinus: 0, 1/2, √2/2, √3/2, 1
- Cosinus: 1, √3/2, √2/2, 1/2, 0
Introduction au tableau des valeurs de cosinus et sinus
Le tableau des valeurs de cosinus et sinus est un outil essentiel en trigonométrie pour les étudiants et les passionnés de mathématiques. Grâce à ce tableau, il est possible d’accéder rapidement aux valeurs remarquables des fonctions trigonométriques pour les angles courants, facilitant ainsi la compréhension des concepts fondamentaux et leur application dans des problèmes réels. Cet article explore les principales caractéristiques du tableau des sinus et cosinus, ainsi que leur utilisation pratique.
Définitions et fonctionnement des fonctions trigonométriques
Avant d’explorer le tableau des valeurs, il est crucial de définir les fonctions sinus et cosinus. Pour un angle donné exprimé en radians ou en degrés, le cosinus correspond à l’abscisse du point sur le cercle trigonométrique, tandis que le sinus correspond à l’ordonnée. Ces définitions sont essentielles pour comprendre les valeurs qui seront présentées dans le tableau.
Les angles communs dans la trigonométrie
Le tableau des valeurs de sinus et de cosinus se concentre principalement sur certains angles remarquables, tels que 0°, 30°, 45°, 60° et 90°. Chacune de ces valeurs mérite d’être mémorisée puisqu’elles apparaissent fréquemment dans des équations trigonométriques. Par exemple, on sait que :
- sin(0°) = 0 et cos(0°) = 1
- sin(30°) = 1/2 et cos(30°) = √3/2
- sin(45°) = √2/2 et cos(45°) = √2/2
- sin(60°) = √3/2 et cos(60°) = 1/2
- sin(90°) = 1 et cos(90°) = 0
Lecture du tableau trigonométrique
Pour utiliser efficacement le tableau des valeurs trigonométriques, il est utile de connaître son agencement. Le tableau est généralement divisé en deux parties : une première pour le cosinus et l’autre pour le sinus. Les valeurs peuvent également être présentées en degrés et en radians, offrant ainsi une flexibilité d’utilisation selon la méthode qui vous convient le mieux.
Importance des signes dans le tableau
Lors de la consultation du tableau, il est important de prêter attention aux signes des valeurs. En fonction du quadrant dans lequel se trouve l’angle, les valeurs de sinus et cosinus peuvent être positives ou négatives. Par exemple, dans le premier quadrant, les deux fonctions sont positives, tandis que dans le deuxième quadrant, le sinus est positif, mais le cosinus est négatif.
Applications pratiques du tableau
Le tableau des valeurs de sinus et cosinus est souvent utilisé pour résoudre des problèmes de géométrie, d’ingénierie et de physique. Par exemple, on peut l’utiliser pour déterminer les projections d’un vecteur, résoudre des triangles, ou encore analyser des ondes. Connaître les valeurs exactes facilitera grandement ces types d’analyses et permettra d’économiser du temps lors des calculs.
Méthodes mémotechniques pour retenir les valeurs
Pour ceux qui trouvent difficile de mémoriser ces valeurs, plusieurs astuces de mémorisation existent. Une méthode courante consiste à se rappeler des résultats des angles en fonction de leur position sur le cercle trigonométrique. Les valeurs peuvent être visualisées comme une séquence de chiffres et de racines carrées, ce qui facilite leur rétention.
L’importance du tableau des valeurs de cosinus et sinus dans l’apprentissage et l’application de la trigonométrie est indéniable. Que ce soit pour des études académiques ou des applications pratiques au quotidien, les connaissances sur ces valeurs permettent de déchiffrer facilement des problèmes mathématiques complexes.